Community structures within neighborhood of a vertex

Networks are ubiquitous and understanding them is very essential while solving problems or inferring something about them. This article covers the importance of community structures in the network and their natural existence in real-world networks. If you don't know anything about graph theory or basic network terminologies I suggest you go through this link.

Fig. (A) Communities present inside Complex Network Wiki-page

The simplest way to study the neighborhood of vertex is the Average Clustering Coefficient(C). The clustering coefficient is the probability that two neighbors of a vertex are connected. In this, we calculate the average over each vertex. But sometimes it can be a very crude way to take an average. Taking average means we are assuming the probability of connection between two neighbors is the same on the entire network. This is not true when we are working with real-world networks(large networks where the number of vertices and edges are large).

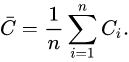
Ci: Clustering coefficient of i’th vertex

So basically what I am saying is that some of the vertices in a network are densely connected than other i.e. the probability that their neighbors are connected is more, not average. This phenomenon leads to a new concept called Community Structures. If someone is saying there are communities inside the network then it means that there are some clusters of vertices inside the network which are tightly connected than others. Communities represent some groups, clusters or partition inside the network.

Importance of community structures:

The existence of communities also generally affects various processes like rumor spreading or epidemic spreading happening on a network. Hence to properly understand such processes, it is important to detect communities and also to study how they affect the spreading processes in various settings. An important application that community detection has found in network science is the prediction of missing links and the identification of false links in the network. During the measurement process, some links may not get observed for many reasons. Similarly, some links could falsely enter into the data because of the errors in the measurement.

Real-world example:

If we consider any article on Wikipedia page, say Mathematics. We can construct a network of the neighborhood of those articles, where articles will be vertices and hyperlinks pointing the articles will be edges in the network. This means there will be edges between two vertices if there is a hyperlink pointing to them. The network here is directed also called Digraph. I have constructed a network of Wikipedia articles by scraping Wikipedia Pages. If you consider some Wikipedia article say mathematics, what are the neighbors of mathematics(from current wiki-page which other wiki-pages you can jump using hyperlinks present on that page) and is there any connection between those neighbors of mathematics (does those neighbors direct to each other). The network created is up-to first neighbors only. This network is constructed by crawling through Wikipedia pages using python packages like BeautifulSoup. If you want to see how does this python code works for creating the network, click here.

Fig. (B) Communities present inside Mathematics Wiki-page

As you can see in Fig. (A) and (B), a real-world network of Wikipedia articles have communities/clusters inside them. The above visualization is made using Gephi tool. I am currently studying changes in the properties of different wiki-pages networks. And how these properties affect the communities of networks. This was part of my Master’s project under Dr. S. M .Shekatkar.

Resources:

Networks, Second Edition, By Mark Newman